개념쏙쏙! 수학
끊임없이 반복되는 길, 뫼비우스의 띠
종이 띠 한 번 꼬아 양 끝을 붙이면
안쪽·바깥쪽 구별이 없는 띠가 돼 두 바퀴 돌면 출발 지점으로 돌아와요
이 띠 가운데 선을 따라 잘라 보면 둘로 나뉘지 않고 네 번 꼬인 띠 돼
길이 늘지만 뫼비우스의 띠는 아니죠
"콜록콜록. 엄마, 추운데 돌아다녔더니 감기 걸린 것 같아요."
"그러니까 엄마가 매일 목도리를 두르고 나가라고 했잖니. 여기 목도리 꺼내놨으니 내일부터는 꼭 두르고 다니렴."
"네, 그럴게요. 어라? 엄마, 이 목도리는 처음 보는 거네요. 모양이 참 신기해요."
목도리는 양끝이 둥글게 연결된 형태였는데, 앞부분이 한 번 꼬여 있었어요.
"얼마 전에 새로 산 것이란다. 기본 일자 목도리를 변형하여 만든 목도리로 '뫼비우스의 띠' 모양을 하고 있지. 목에 두르면 자연스럽게 멋스러운 모양이 잡히는 데다 따뜻하기까지 하단다."
"뫼비우스의 띠라고요? 책에서도 본 적 있고, 많이 들어본 말이기도 해요."
"그럼 이번 기회에 뫼비우스의 띠가 무엇인지 정확하게 알아볼까?"
"네! 좋아요."
-
- ▲ 그림=이창우
"직사각형 종이 띠를 둥글게 말아서 양 끝을 그대로 붙여보렴. 어떤 모양이 만들어졌니?"
"원통 모양이 나왔어요. 이 원통은 안과 밖이 뚜렷하게 구별되네요."
"자, 이번엔 같은 종이 띠를 한 번 꼬아서 양끝을 붙여보렴. 색다른 모양이 나올 거야."
와~ 종이 띠를 한 번 꼬아서 붙이니 아까 엄마께서 주신 목도리와 같은 모양이 나왔어요.
"이러한 모양을 뫼비우스의 띠라고 해. 이 도형을 연구한 독일 수학자 뫼비우스의 이름을 딴 것이지."
"언뜻 보기에는 단순한 모양인데 왜 유명한 거예요? 특별한 성질을 가지고 있나요?"
"물론이지. 가장 큰 특징은 바깥쪽과 안쪽의 구별이 없다는 점이란다. 어느 지점에서나 띠의 중심을 따라 한 바퀴 돌면 출발한 곳의 정반대 면에 도달하지. 이때 계속 나아가서 두 바퀴를 돌면 처음의 출발 위치로 돌아오게 돼. 즉, 뫼비우스의 띠는 안과 밖의 구분이 없는 끊임없는 반복을 의미하지."
엄마의 설명을 듣고 제가 만든 뫼비우스의 띠에 직접 실험해 봤어요. 뫼비우스의 띠 가운데 한 지점에서 연필로 선을 그어나가기 시작했지요. 와~ 정말로 한 바퀴를 도니 출발점의 반대 면에, 두 바퀴를 도니 출발점에 도착했어요.
"정말 신기하네요. 엄마, 또 다른 성질은 없어요?"
"당연히 있지. 뫼비우스의 띠 가운데를 자르면 어떻게 될 것 같니?"
"에이~ 당연히 둘로 나뉘겠지요."
"그럴 것 같지? 그럼 직접 뫼비우스의 띠 가운데 선을 따라 잘라봐."
"어라? 직접 잘라보니 네 번 꼬인 띠 하나가 되네요. 대신 길이가 2배로 길어졌어요. 그래도 끊어지지 않고 하나로 연결이 되어 있으니까 이것도 뫼비우스의 띠 맞지요?"
"아쉽게도 이 고리는 더는 뫼비우스의 띠가 아니란다. 안쪽과 바깥쪽이 명확히 구분되기 때문이지. 뫼비우스의 띠에 대해 더 자세히 알아볼까? 사실 뫼비우스의 띠는 띠가 꼬인 횟수에 따라 결정된단다. 홀수 번 꼬인 띠는 안과 밖의 구분이 없는 뫼비우스의 띠가 되지만, 짝수 번 꼬인 띠는 안과 밖이 구분되기 때문에 뫼비우스의 띠가 아니야. 또 꼬인 횟수에 따라 가운데 선을 따라 잘랐을 때의 모양도 달라진단다. 조금 전 한 번 꼬인 뫼비우스의 띠를 자르니 띠의 개수는 여전히 한 개이지만 길이는 2배가 되었지? 이처럼 홀수 번 꼬인 띠를 이등분하면 띠 개수는 하나지만 길이가 2배가 된단다. 이와 달리 짝수 번 꼬인 띠를 이등분하면 띠가 2개로 나뉘지."
"간단해 보이는 띠에 많은 특징이 있네요."
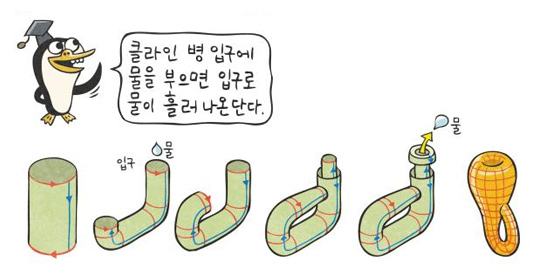
"뫼비우스의 띠와 같이 안과 밖의 구분이 없는 도형으로 '클라인 병'이란 것도 있어. 클라인 병은 밑면과 윗면이 뚫려 있는 원기둥으로 만들 수 있는데, 원기둥의 한쪽 끝이 원기둥의 옆면을 뚫고 들어가서 뚫고 들어간 쪽의 끝이 다른 쪽과 만나게 하면 클라인 병이 된단다. 재미있는 것은 클라인 병을 반으로 자르면 뫼비우스 띠 2개를 얻을 수 있다는 것이지."
"와~ 정말 신기하네요. 그런데 우리 주변에서 뫼비우스의 띠 형태로 된 것을 더 찾아볼 수 있나요?"
"그럼. 앞과 뒤가 구별되지 않는다는 특성 때문에 산업에서도 많이 활용되고 있단다. 마트 계산대, 공항 검색대 등에서 볼 수 있는 컨베이어 벨트 중에는 뫼비우스 띠 모양으로 된 것이 많아. 왜냐하면 벨트를 그대로 거는 것보다 쉽게 빠지지 않고, 벨트가 돌아갈 때 양쪽 면이 고르게 쓰여 벨트 수명도 길어지기 때문이지. 또 전 세계적으로 통용되는 재활용 마크도 뫼비우스의 띠로 되어 있어. 어느 지점에서나 띠의 중심을 따라 이동하면 처음 위치로 돌아온다는 특징과, 이미 사용한 자원을 다시 사용한다는 재활용의 의미가 잘 맞아떨어지기 때문이지."
"정말 많은 곳에 쓰이고 있었네요. 내일은 목도리를 하고 가서 친구들한테 자랑하고, 오늘 뫼비우스의 띠에 대해 배운 내용도 설명해 줄래요."
[함께 풀어봐요]
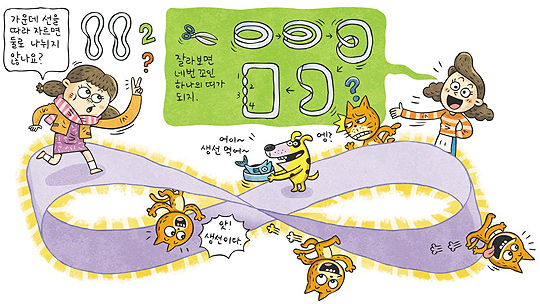
뫼비우스의 띠를 3등분하려고 합니다. 어떻게 될지 예상해 보고, 직접 종이를 오려 확인해 보세요.
해설: 뫼비우스의 띠를 3등분하면 두 띠로 분리됩니다. 하나는 원래 띠와 길이가 같은 뫼비우스의 띠가 되고, 다른 하나는 길이가 두 배로 길고 네 번 꼬인 띠가 되지요.
[관련 교과] 4학년 1학기 '규칙 찾기' 6학년 1학기 '여러 가지 입체도형'