신문은 선생님
[수학 산책] 다리를 한 번씩만 건너서 7개 다리를 모두 건널 수 있을까?
입력 : 2021.09.09 03:30
오일러의 '한붓그리기 법칙'
-
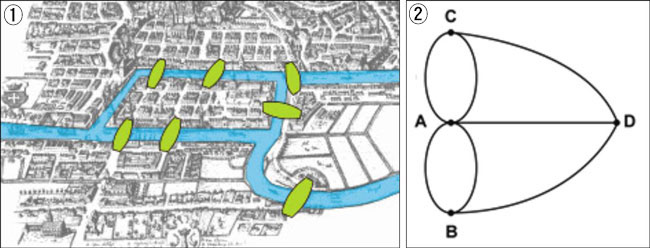
- ▲ /위키피디아·이광연 제공
수학에도 유명한 다리가 있어요. 러시아 쾨니히스베르크(현재 칼리닌그라드)에는 프레골랴강이 흐르고 있어요. 이 지역은 본래 프로이센공국의 수도로 독일 철학자 이마누엘 칸트의 고향이기도 해요. 그곳엔 18세기 때부터 다리 일곱 개<그림1>가 놓여 있었는데, 당시 어떤 사람이 '다리를 한 번씩 건너서 다리 일곱 개를 모두 건널 수 있을까'라는 수수께끼를 냈어요. 붓을 떼지 않고 같은 곳을 두 번 지나지 않고 도형을 그리는 '한붓그리기' 문제였죠. 많은 시민들이 이 문제에 도전했지만 모두 실패했어요. 어떤 사람은 모든 다리를 일일이 걸어다니며 풀려고 했는데도 못 풀었대요.
그때 이 문제를 보고 "불가능하다"고 단언한 사람이 있었어요. 스위스 출신 천재 수학자 레온하르트 오일러(1707~1783)였어요. 오일러는 7개 다리가 놓인 지도를 추상화해서 간단하게 만들었어요. 다리는 '선'으로, 다리가 잇는 땅은 '점'으로 만들었어요. <그림2>처럼요. 그리고 여기서 한붓그리기가 가능한 법칙을 발견했어요. 그 법칙은 ▲모든 점이 짝수 개의 선과 연결되거나 ▲두 개의 점만 홀수 개의 선과 연결되어야 한다는 것이었죠. 이 쾨니히스베르크의 7개 다리는 네 점이 모두 홀수 개의 선과 연결되어 있었기 때문에 한붓그리기가 불가능하다는 결론을 내린 거예요. 오일러는 이를 정리해서 1735년 논문으로 발표했어요.
오일러의 이 논문은 추후 다른 수학자들에 의해 '그래프 이론'으로 발전했답니다. 그래프 이론은 '점'과 '변'의 결합 양식에 대한 이론이에요. 여기서 그래프는 우리가 일반적으로 떠올리는 4분면 위에 그려진 막대 그래프나 선 그래프와는 달라요. 예를 들어, 각 정거장이 점으로 그려져 있고, 이를 선으로 연결한 '버스 노선도'나 '지하철 노선도'가 그래프랍니다. 또 우편물을 최소 시간으로 배달할 수 있는 최적의 경로를 찾는 데도 그래프 이론을 활용할 수 있어요. 그래프 이론은 최근엔 첨단 과학 분야에도 많이 활용되고 있어요. 컴퓨터 프로그램을 짤 때나 코로나 같은 바이러스의 전파 경로를 탐색할 때 등에도 이용된다고 합니다.
