신문은 선생님
[수학 산책] 피타고라스가 증명하기 500년 전에 출간된 고대 중국 수학책에도 나온대요
피타고라스의 정리
사실 이 정리는 고대 그리스 수학자 피타고라스(기원전 580~500)가 처음 만든 게 아니랍니다. 기원전 3000년쯤 메소포타미아 사람들도 세 변 길이의 비가 3, 4, 5이거나 5, 12, 13인 삼각형이 직각삼각형이라는 것을 알고 있었고, 이 직각삼각형 세 변의 길이 가운데 작은 두 수의 제곱의 합이 큰 수의 제곱과 같다는 것도 알았어요. 또 피타고라스가 활약했던 시대보다 500년 앞선 기원전 10세기 고대 중국 수학책인 '주비산경'에는 이 정리가 소개돼 있답니다. 이를 오늘날 '구고현의 정리'라 불러요.
-
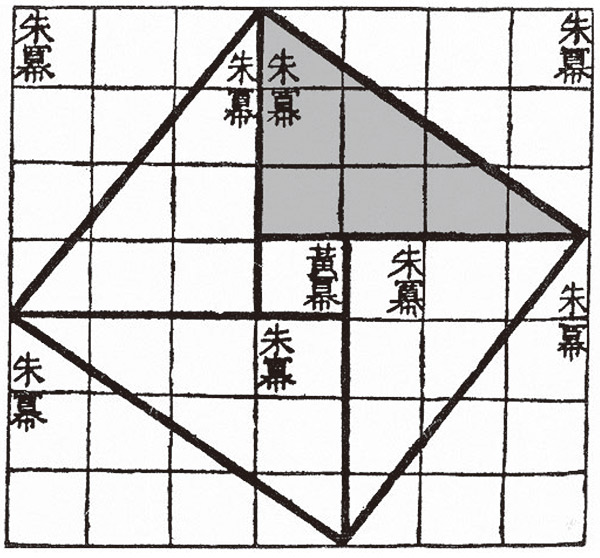
- ▲ 고대 중국 수학책에 실려있다는 ‘구고현의 정리’예요. 밑변의 길이가 3이고 높이가 4인 직각삼각형(색칠한 부분)의 빗변의 길이는 5가 된다는 내용입니다. /위키피디아
이 정리는 어떤 수식도 없이 바둑판 무늬 그림 한 장으로 이 공식을 증명하고 있어요. 밑변(구)의 길이가 3이고 높이(고)가 4인 직각삼각형의 빗변(현)의 길이는 5가 된다는 것이죠. 큰 마름모 안에 작은 정사각형이 25개가 있기 때문에 한 변(빗변)의 길이가 5라는 거예요. 그래서 구고현의 정리를 수학자들은 '세상에서 가장 아름답고 완벽한 증명법'이라고 불러요.
피타고라스는 그리스 사모스섬에서 태어났어요. 이탈리아 남부 크로톤에 학교를 세우고 제자들을 길렀죠. 당시 피타고라스는 '만물의 근원은 수(數)'라고 주장했는데요. 그는 수학을 엄밀한 증명을 통해서만 완성되는 학문이라 생각했어요. 그래서 그때까지 직관적으로 이용되던 직각삼각형 세 변 사이의 관계를 수학적으로 엄밀하게 증명했고, 그 업적 때문에 이 공식에 피타고라스의 이름을 붙이게 된 거예요.
그렇다면 피타고라스는 어떻게 이 공식을 정리할 수 있었을까요? 당시 그리스 건축물 바닥 타일과 관련이 있다는 설이 있어요. 피타고라스가 살던 시대에는 건축물 바닥을 정다각형 타일로 까는 방식이 추진되고 있었다고 해요. 이를 눈여겨보던 피타고라스가 직각이등변삼각형에서 피타고라스의 정리가 성립하고 있음을 발견하고 이를 직각삼각형으로 일반화했다는 것이죠.
피타고라스는 특히 누구나 공감하고 인정할 수 있는 증명법을 이용해서 수학 공식을 만들었는데, 오늘날 피타고라스의 정리에 관한 증명은 닮은꼴 삼각형을 이용한 방식 등 약 400여 가지에 이르러요. 수학에 흥미를 갖고 있는 많은 사람들이 계속해서 다양한 증명법을 찾았지요. 우리가 잘 알고 있는 르네상스 시대 거장인 레오나르도 다빈치도 피타고라스의 정리를 새로운 방법으로 증명했고, 미국의 20대 대통령인 제임스 가필드(1831~1881)도 자신만의 새로운 증명법을 제시했답니다.
