신문은 선생님

"환율 상승으로 경제성장이 기대되고 있습니다."

"환율상승? 그게 무슨 뜻이지요?"

아빠와 함께 뉴스를 보던 영운이가 처음 듣는 용어가 나오자 궁금해했어요.

"환율이란 서로 다른 화폐를 교환할 때 사용하는 비율이야. 예를 들어, 우리가 미국으로 여행을 간다고 할 때 미국에서 우리나라 돈을 그대로 사용할 수 없겠지? 그럼 어떻게 해야 할까?"

"우리 돈을 미국 돈으로 바꿔야지요. 아, 그러니까 환율이란 건 우리나라 돈 얼마를 미국 돈 얼마로 바꿀 수 있는지 알려주는 거군요?"

"맞아. 보통 우리나라에서 환율이라고 하면 1달러와 교환할 수 있는 금액(원화)을 의미해. 자, 지금 환율이 약 1200원이구나. 그리고 환율이 상승했다는 것은 1달러와 교환하는 데 필요한 금액이 이전보다 더 커졌다는 걸 의미하는 거야."

"어? 그럼 우리 돈의 가치가 더 떨어졌다는 거잖아요? 그런데 왜 경제성장이 기대된다는 거죠?"

"그건 환율이 원화 가치와는 반비례 관계에 있지만, 수출과는 정비례 관계에 있기 때문이지."

"예? 반비례? 정비례? 이것도 처음 듣는 용어예요."

"어떤 식에서 어떤 값이 2배, 3배, 4배로 늘어날 때 다른 값도 2배, 3배, 4배로 늘어가거나 혹은 1/2배, 1/3배, 1/4배로 줄어드는 것, 즉 일정한 비율로 변하는 것을 비례라고 해. 이때 늘어나는 관계를 정비례, 줄어드는 관계를 반비례라고 하지. 이런 관계는 일상생활에서 쉽게 찾아볼 수 있어. 예를 들어, 네가 매일 1000원씩 통장에 저축한다고 하자. 그럼 날짜가 지날수록 저축액이 늘어나겠지? 그럼 1년 동안 저축하면 저축액은 얼마가 될까?"

"음. 1년이 365일이니까 36만5천원이네요."

"그래. 하루 저축액에 저축일자를 곱하면 전체 저축액을 쉽게 구할 수 있지? 그럼 하루 저축액을 a, 저축일자를 x, 전체 저축액을 y라고 두고 식을 만들어 볼래?"

"y=a×x가 되겠네요?"

"그래. 이 식은 (a가 0이 아닐 때) x값이 2배, 3배… 늘어날수록 y값도 2배, 3배… 늘어난다는 특징을 가지고 있지. 이렇게 비교되는 두 값의 관계가 같은 비율로 증가하는 것을 정비례라고 하는 거야. 그럼 이와 같은 관계를 가진 상황을 우리 주변에서 더 찾아볼까?"

"음. 사려는 물건이 많으면 내야 하는 금액이 많아지는 것? 오래 걷거나 빨리 달릴수록 더 멀리 갈 수 있는 것?"

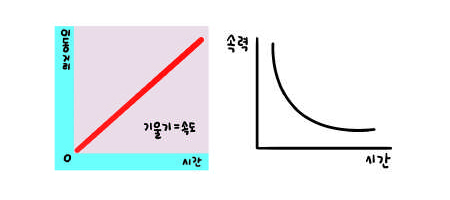
"예시를 잘 찾은 걸 보니 이해를 잘한 것 같구나. 그런데 그런 상황을 잘 살펴보면 늘어나는 요소와 더불어 줄어드는 요소도 있다는 걸 알 수 있어. 네가 말한 첫 번째 상황에서는 물건의 개수와 지불 금액은 서로 같은 비율로 늘어나는 관계에 있지만, 만약 쓸 수 있는 돈이 정해져 있다면 물건의 값과 개수는 서로 같은 비율로 줄어드는 관계에 있지. 예를 들어 1만원만 쓸 수 있다면 물건 값이 1000원일 때 10개를 살 수 있고, 2000원일 때는 5개, 5000원일 때는 2개로 물건 값이 비쌀수록 살 수 있는 물건의 개수는 일정한 비율로 줄어들어. 이런 관계는 정비례와 반대되는 관계라고 하여 반비례라고 한단다. 정비례와 반비례를 그래프로 그리면 이런 특징이 나타나."

"아, 걷는 시간이 길어지면 걸어간 거리는 늘어나지만, 속력이 빨라지면 도착하기까지의 시간은 줄어드네요."

"그래. 이동거리를 구하는 식은 '거리=시간×속력'인데 이 식은 '속력=이동거리/시간'으로도 바꿀 수 있지. 여기서 비교되는 요소를 x와 y로 놓는다면 y=a/x가 되지? 이러한 식이 만족하는 경우 x와 y는 반비례 관계에 있다고 해. 그럼 피자 8조각이 있는데 사람의 숫자가 x명일 때 1인당 나눠 먹을 수 있는 피자 조각 수 y를 식으로 만들어볼래?"

"전체 피자 조각을 사람 수대로 나눠야 하니 y=8/x네요. 이제 정비례, 반비례에 대해 확실히 이해했어요."

"그럼 다시 환율과 경제성장의 관계를 생각해 볼까? 경제성장은 수출과 관계가 깊어. 수출을 많이 한다는 것은 그만큼 다른 나라로부터 금전적인 이익을 많이 얻는다는 것을 의미하니까. 그런데 수출은 환율과 밀접한 관계에 있지. 예를 들어 환율이 1달러에 1000원이라고 하자. 그럼 다른 나라에서는 우리가 만든 1000원짜리 제품을 1달러에 구매할 수 있어. 그런데 환율이 1500원으로 올라가면 다른 나라에서는 3000원짜리 제품을 3달러가 아닌 2달러로 살 수 있잖아? 이렇게 되면 마치 할인하는 제품이 더 잘 팔리는 것처럼 수출이 늘어날 수 있어. 반대로 우리 입장에서는 1만원이면 살 수 있었던 10달러짜리 제품을 1만5000원에 사야 하니 부담이 커져서 수입은 줄어들게 되지. 즉, 수출은 늘어나고 수입은 줄어들어 경제가 성장하는 거야."

"아. 그래서 환율은 수출에 정비례하고 원화 가치에는 반비례한다고 하셨군요?"

"그래. 하지만 엄밀히 말하면 사회 용어로 사용되는 비례와 수학에서 사용되는 비례는 같지 않아."

"예? 같지 않은데 같은 용어를 쓴다고요?"

"그래. 수학적인 비례는 앞서 이야기했다시피 정확한 비율로 변화할 때만 비례라고 할 수 있어. 그런데 환율이 높아지면 수출이 유리해지는 건 맞지만, 환율이 2배, 3배 높아진다고 해서 수출이 2배, 3배 늘어나는 것은 아니거든. 게다가 제품 품질이 나쁘다면 아무리 가격이 싸져도 수출이 늘어나지 않을 수 있지. 하지만 정비례와 반비례라는 용어를 사용하면 두 요소의 성격을 쉽게 설명할 수 있단다."

[함께 생각해봐요]

어느 공장에서 8명의 직원이 같은 빠르기로 일을 한다고 할 때, 주문받은 일을 완전히 마치는 데, 12일이 걸린다고 해요. 만약 같은 일을 6일 만에 끝내려면 직원은 몇 명이 필요할까요?

답: 16명(8명의 직원이 12일 동안 일하는 양은 96이라고 할 수 있어요. 즉, 일의 양이 일정할 때 직원이 많을수록 일을 마치는 데 걸리는 시간이 짧아지기 때문에 직원의 수와 시간은 서로 반비례 관계에 있어요. 따라서 직원 수=일의 양/걸리는 시간 --〉 직원 수=96/6 즉, 16명)

[관련 교과] 5학년 2학기 '비와 비율'