신문은 선생님

용원이는 요즘 들어 기분이 좋습니다. 얼마 전 조카가 태어났기 때문이죠. 학교를 마치고 집에 오자마자 용원이는 아빠에게 말했어요.

"아빠, 저 기분이 매우 좋아요! 새로 생긴 조카한테 선물을 만들어 주고 싶어요!"

"그래? 그럼 아기 방에 걸어줄 '모빌'을 만들어 보는 건 어떨까?"

"좋아요! 그런데 모빌을 늘 보기만 했지 직접 만들어 보진 않아서 어떻게 하는지 잘 모르겠어요."

"모빌은 철사나 막대 등을 실로 연결하여 매달아 놓은 장식품을 말한단다. 무슨 물건을 막대에 매달지, 무엇으로 연결할지도 중요하지만, 무엇보다 중요한 것은 따로 있단다."

"모빌이 예쁘게 매달려 있기만 하면 되지, 다른 것이 뭐가 중요해요. 저는 아기들이 좋아할 동물 인형과 제가 좋아하는 로봇을 매달래요!"

이것저것을 실에 마구잡이로 연결하고 나서, 막대와 연결된 실을 들어 올렸지만 용원이의 모빌은 자꾸만 한쪽으로 기울어졌습니다.

"아빠, 제가 잘못했어요. 어서 모빌의 비밀을 알려주세요."

"그래, 모빌에서 가장 중요한 것은 바로 '무게중심'이란다. 이 무게중심을 잘 이용해야 모빌이 한쪽으로 기울어지지 않고 평형을 잘 유지하게 되지."

"무게중심이면 무게의 중심을 말하는 건가요?"

"그래. 모든 물체는 지구가 잡아당기는 중력의 영향을 받는단다. 그런데 물체의 모양 또는 형태 등에 따라 물체의 각 지점에 작용하는 힘이 모두 다르단다. 예를 들어 국자는 정중앙을 받치게 되면 무거운 국자 머리 쪽이 국자 손잡이 쪽보다 더 큰 중력을 받게 되어 기울어지게 되는 것과 같은 원리지. 국자가 중심을 유지하게 하려면 무거운 쪽과 가까운 지점에 손가락을 올려 받쳐보면 된단다."

직접 국자를 받쳐본 용원이는 놀라 말했습니다.

"우와, 정말로 국자가 기울어지지 않고 안정적으로 누워있게 되네요!"

▲ /그림=나소연

"그래, 무게중심이라는 것은 물체의 여러 위치에 작용하는 중력과 받치는 힘, 이런 것이 합쳐져서 힘을 전혀 받지 않는 지점을 말하지. 그래서 그 점을 받치게 되면 힘이 어느 한쪽으로 치우치지 않고 공평하게 나누어져 물체가 평형을 이루게 되는 지점을 말하는 거란다. 보통 정다각형 판이라면 무게중심이 도형의 중심이 되곤 하지만 일반적으로 모양만 보고 무게중심을 찾기는 쉽지 않단다."

"그럼 모빌은 어떻게 무게중심을 찾아야 해요? 모빌에 걸게 될 여러 가지 물체의 무게는 다 다를 텐데…."

"그럼 모빌 하나를 만들면서 어떻게 무게중심을 찾아야 할지 생각해보자꾸나. 막대와 실, 그리고 무게가 같은 모빌 조각을 이용해 볼까? 먼저 양쪽 끝에 모빌 조각을 하나씩 걸었다면 어디에 실을 걸어야 평형을 유지할까?"

"어쩐지 정중앙에 걸면 될 것 같아요! 양쪽 무게가 같으니까요!"

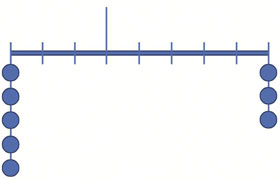
"그래. 그럼 문제를 조금 어렵게 바꿔보자. 한쪽에는 무게가 같은 모빌 조각 두 개를 걸었다면, 다른 한쪽에는 무게가 같은 모빌 한 조각을 어느 지점에 걸어야 모빌이 수평을 이룰까?"

"음. 이건 잘 모르겠어요. 가운데에 걸면 분명히 한쪽으로 치우칠 것 같고…. 국자를 생각해 보면 무거운 쪽에 실이 더 가까워야 할 것 같기는 한데 정확하게는 모르겠어요."

▲ /그림=나소연

"그래. 이렇게 양쪽에 다른 무게를 걸 때는 쉽지가 않지. 이럴 때는 매달린 물체의 무게 합과 무게중심까지 거리의 곱이 좌우가 같으면 평형을 이룬단다. 예를 들어, 매달린 물체 하나의 무게가 10g이라고 한다면 두 개 달린 쪽은 20g이겠지. 자, 이때 무게중심에서 물체 한 개가 매달린 곳까지 거리를 □㎝, 물체 2개가 매달린 곳까지 거리를 △㎝라고 해보자."

"음, 물체의 무게와, 무게중심까지 거리의 곱을 먼저 구해야겠어요. 그리고 각각 구한 것이 좌우로 같아야 하니까, 10×□=20×△이네요." "이 식을 통해 보면 □는 항상 △의 두 배가 되어야 한다는 것을 알 수 있지. 즉 무게중심이 있어야 할 곳은 □까지 길이가 △까지 길이의 두 배가 되는 지점이어야 한다는 뜻이란다. 이런 원리를 이용하면 반대로 미리 줄을 특정 지점에 매달아 놓고 각각의 위치에 어떤 무게의 모빌 조각을 매달아야 평형을 맞출 수 있을지도 알아맞힐 수 있지."

"우와, 정말 신기해요."

"그래, 무게중심에 맞게 물체를 걸어야 모빌이 평형을 이룬단다. 물론, 때에 따라서 더 아름다운 모빌을 만들고자 무게중심에 어긋나게 모빌을 걸기도 하지만, 그런 사람들도 모두 무게중심을 잘 알고 이용하기 때문에 아슬아슬하게 움직이는 모빌을 만들 수 있는 거란다. 이제 용원이도 조카한테 선물로 줄 모빌을 만들어볼까?"

[관련 교과] 4학년 1학기 '혼합 계산', 4학년 1학기 '무게 재기'

[함께 생각해봐요]

용원이는 조카에게 줄 모빌을 만들기 위해 길이가 30㎝인 막대에 무게가 5g인 모빌 조각들을 매달려고 합니다. 막대의 왼쪽 끝에는 모빌 조각 5개를, 오른쪽에는 모빌 조각 3개를 달았습니다. 마지막으로 천장에 매달 실을 무게중심에 묶으려고 한다면, 오른쪽으로부터 몇 ㎝ 지점에 실을 매달아야 할까요?

풀이: 모빌이 평형을 이루려면, 무게중심으로부터 거리와 무게를 곱한 값이 양쪽 모두 같아야 합니다. 즉, 양쪽의 무게와 거리의 곱이 같으려면 아래 그림과 같은 형태여야 합니다. 따라서 30㎝를 8등분한 뒤 오른쪽에서 5배 되는 지점을 무게중심으로 잡아 실을 매달면 되므로, 30×5/8=75/4㎝인 지점에 실을 매달면 됩니다.