신문은 선생님

"아빠. A2 복사 용지 크기가 얼마나 되나요?"

"갑자기 그건 왜 묻지?"

"방학 숙제가 A2 용지에 가족 신문을 만드는 건데, 문구점에 A2 용지가 없다고 해서 전지를 샀거든요? 전지를 A2 용지 크기로 잘라서 쓰려고요."

"그런데 형식아. 너 A4 용지가 뭔지 알지?"

"네. 프린터로 인쇄할 때 쓰는 종이잖아요? 그러고 보니 A2랑 이름이 비슷하네요! 무슨 관련이 있는 건가요?"

"물론 관련이 있지. A0란 종이를 몇 번 2등분했는가에 따라 붙인 이름이니까. 쉽게 말해 A1은 A0를 한 번, A2는 두 번, A3는 세 번, A4는 네 번 2등분한 크기야."

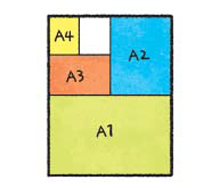
"어? 그럼 A2는 A4의 4배 크기인가요? 그럼 A4 용지를 4개 붙이면 A2 용지가 되는 거네요?"

"맞아. 금방 이해했구나. 신기하지 않니? A2, A3, A4 용지가 서로 닮은꼴, 즉 크기만 다르고 모양이 같은 도형이란 점이 말이지."

"어? 한 종이를 계속 반으로 잘랐으니 당연한 거 아닌가요?"

"당연하다니? 휴지 한 칸을 반으로 접어 봐라. 원래 휴지 모양과 비교할 때 서로 같은 모양으로 보이니?"

"아. 아니요. 그러고 보니 2번 잘랐을 때는 같은 모양이 나와도 1번 잘랐을 때는 다른 모양이 나오네요."

"맞아. 모든 직사각형은 짝수 번 2등분했을 때 닮은꼴이 만들어지지만, 홀수 번 2등분했을 때 정확히 닮은꼴이 되는 경우는 짧은 변과 긴 변의 비가 1:√2 (루트 2)가 되는 경우뿐이야."

"그런데 루트가 뭐죠? 처음 들어보는 용어인데요?"

"루트란 제곱근이라고 부르는데, 제곱했을 때 √(루트) 안의 수가 나오는 수를 의미해. 예를 들어 √4 를 보면, 제곱해서 4가 되는 수는 2지. 즉 √4 는 2인 거야. 그럼 √9 를 구해 볼 수 있겠니?"

"3 곱하기 3은 9니까. 답은 3이네요? 생각보다 쉬운데요? 그럼 √2 는 제곱해서 2가 되는 수니까…. 아, 이건 못 구하겠어요."

"하하. 당연하지. 그건 수학 선생님도 계산하기 어려운 문제니까. 계산기도 화면에 표시할 수 있는 부분까지만 나타낼 수 있을 정도로 소수점 아래 수가 끊임없이 나타나지. 1.41421356237…로 말이야. 그래서 같은 수는 헤아릴 수 없다는 의미로 '무리수'라고 부른단다."

"그런데 왜 A4 용지에 그런 비율이 있는 거지요?"

"그것은 자르고 또 잘라도 처음 종이와 모양이 닮은 종이를 만들려고 수학적 계산을 했기 때문이야. 잘랐을 때도 같은 모양이라면 용지를 다양하게 활용할 수 있을 테니까. 낭비하는 종이양도 줄이고. 자, 직사각형인 두 도형이 닮은꼴이 되려면 가로변과 세로변 비율이 같아야 해. 예를 들어 가로 5, 세로 2인 직사각형은 가로와 세로 비는 5:2고 비율은 5/2 즉, 2.5지. 이와 닮은꼴이 되는 도형은 모두 가로와 세로 비율이 2.5가 되어야 해. 자. 그러면 이 도형과 닮은꼴인 직사각형의 가로 길이가 6이라면 세로 길이는 얼마가 될까?"

"6/□=2.5가 되어야 하니까. 세로 길이는 6/2.5가 되겠네요! 답은 2.4예요."

"오, 잘했다. 자, 그럼 직사각형 종이가 있다고 했을 때, 짧은 변을 x라고 하고 긴 변을 y라고 해 보자. 그럼 그것을 반으로 자른 종이는 짧은 변이 y/2가 되고 긴 변은 x가 되겠지?"

"네. 긴 변은 반으로 잘려 짧은 변이 되고, 짧은 변이었던 부분은 긴 변이 되니까요."

"그래. 그럼 두 도형이 닮은꼴이라면 x:y=y/2:x가 성립해야 해. 그럼 이 비례식의 내항과 외항을 곱하면 x×x=y×y/2가 되지. 여기에 아까 배운 루트를 각 항에 씌워봐."

"아. x제곱의 제곱근은 x가 되니까, x=y/√2 가 되겠네요?"

"그래 그럼 바로 y/x라는 값이 나오지. 그래서 긴 길이/짧은 길이의 비율이 1.4142135…가 되는 경우를 찾아 용지를 만든 거야. 복사 용지나 공문서 등에 가장 많이 쓰는 A4 용지는 가로 210㎜, 세로 297㎜로 되어 있어. 계산기로 한번 계산해 보렴."

"1.414285714… 와~. 소수점 아래 넷째 자리까지 일치하네요."

"그래 이건 1/10000㎜까지 정밀하다는 거지. A4 용지 두 장을 붙인 A3는 가로 297㎜, 세로 420㎜잖아? 이것을 계산기로 계산해 보면 1.41414…로 소수점 아래 셋째 자리까지 일치해."

"우아 정말 신기하네요."

"자, 이젠 충분히 A2 용지를 만들어 가족 신문을 만들 수 있겠지?"

"네. 오늘 배운 내용도 꼭 가족 신문에 실어야겠어요. 제목은 '형식이, A4 용지로 제곱근을 배우다'."

"하하. 그거 정말 좋은 아이디어구나."

[함께 생각해봐요]

원의 넓이가 2배가 되도록 하기 위해서는 반지름의 길이를 몇 배로 만들면 될까요?

풀이: 원의 넓이는 반지름×반지름×원주율(3.14)이에요. 여기서 보면 반지름이 두 번 곱해지는 형태이기 때문에 반지름이 2배가 되면 원의 넓이는 4배가 된답니다. 즉, 원의 넓이가 2배가 되도록 하기 위해서는 반지름에 제곱했을 때 2가 되는 수, √2 배를 해 주면 됩니다.

[관련 교과] 5학년 2학기 '비와 비율'