신문은 선생님
[개념쏙쏙! 수학] 다양한 도형, 어떻게 하면 똑같이 나눌 수 있을까
입력 : 2015.07.30 03:06
초기 인류, 원뿔 형태 집 짓고 살다 넓어진 집의 공간 활용 높이기 위해 사각기둥 형태의 집 짓기 시작해요
도형, 같은 모양·크기로 분할하려면 나눠야 하는 수의 배수만큼 잘라야
"저 아파트 좀 봐요. 모양이 신기해요."
아빠와 손을 잡고 길을 걷던 영민이는 새로 지은 아파트의 모양이 신기한지 발걸음을 멈추고 이리저리 둘러봤어요.
"그래. 사각기둥 모양에서 벗어나 다양한 모양으로 지어진 건물을 보니 신기하게 보이는구나."
"맞아요. 그런데 왜 대부분의 아파트, 빌딩은 사각기둥 모양으로 만든 것일까요?"
"그것은 공간을 활용하기 쉽기 때문이야."
"공간 활용요?"
아빠와 손을 잡고 길을 걷던 영민이는 새로 지은 아파트의 모양이 신기한지 발걸음을 멈추고 이리저리 둘러봤어요.
"그래. 사각기둥 모양에서 벗어나 다양한 모양으로 지어진 건물을 보니 신기하게 보이는구나."
"맞아요. 그런데 왜 대부분의 아파트, 빌딩은 사각기둥 모양으로 만든 것일까요?"
"그것은 공간을 활용하기 쉽기 때문이야."
"공간 활용요?"
-
![[개념쏙쏙! 수학] 다양한 도형, 어떻게 하면 똑같이 나눌 수 있을까](http://newsteacher.chosun.com/site/data/img_dir/2015/07/29/2015072903818_0.jpg)
- ▲ /그림=이창우
"아, 나누다 보니 원형인 집은 모서리 부분이 둥글어서 나누었을 때 뭔가 좁아지는 것 같은 느낌이 들어요."
"그렇지? 사각형은 여러 개의 사각형으로 분할할 수 있지만, 원은 같은 모양으로 분할하기 어렵지. 그리고 모서리가 둥글어지면 가구를 놓을 때 쓸모없는 공간이 생겨서 공간을 충분히 활용하기가 어렵지."
"아. 그래서 대부분의 건물이 사각기둥으로 되어 있는 거구나."
-
![[개념쏙쏙! 수학] 다양한 도형, 어떻게 하면 똑같이 나눌 수 있을까](http://newsteacher.chosun.com/site/data/img_dir/2015/07/29/2015072903818_1.jpg)
- ▲ /그림=이창우
"아. 정사각형 3개니까 3가구라면 쉽게 나눌 수 있는데 4가구로 나누려 하니 어렵네요. 게다가 모양과 크기도 같아야 한다니…."
"하하. 우선 정사각형의 땅을 3가구에 똑같이 나누어 주는 문제를 생각해 보자. 정사각형은 반으로 나누면 2개의 직사각형이 되고 다시 반으로 나누면 4개의 정사각형이 되지. 이렇게 나누다 보면 짝수로만 나누어지게 되는데, 한 변을 3등분하면 홀수인 9개의 정사각형으로 나눌 수도 있어. 9는 3으로 나누어떨어지는 수, 즉 3의 배수이 때문에 이렇게 3가구에 똑같이 나누어줄 수 있지."
-
![[개념쏙쏙! 수학] 다양한 도형, 어떻게 하면 똑같이 나눌 수 있을까](http://newsteacher.chosun.com/site/data/img_dir/2015/07/29/2015072903818_2.jpg)
- ▲ /그림=이창우
"잘했어. 그럼 정말 같은 모양으로 4분할을 할 수 있는지 볼까?"
"성공했어요. 도형을 여러 개의 같은 도형으로 나누어보니 같은 모양과 크기로 나눌 수 있는 방법을 찾을 수 있네요!"
"좋아. 이번엔 똑같은 'ㄴ'자 모양으로 9세대에 나누어줄 수 있도록 분할해 볼래?"
-
![[개념쏙쏙! 수학] 다양한 도형, 어떻게 하면 똑같이 나눌 수 있을까](http://newsteacher.chosun.com/site/data/img_dir/2015/07/29/2015072903818_3.jpg)
- ▲ /그림=이창우
"잘했어. 그럼 이번에는 정삼각형 6개로 만들어진 스핑크스 모양의 도형을 4개의 같은 도형으로 만들어 볼래?"
"앗. 그게 정말 가능한가요? 음…. 우선 정삼각형을 분할하여 정삼각형을 만들 수 있는 방법이 있는지 생각해 봐야겠네요. 앗, 정삼각형 안에 작은 정삼각형을 거꾸로 그리면(각 변의 중심점을 선으로 연결하면) 4개의 정삼각형이 만들어져요. 그럼 정삼각형이 6개니까 작은 정삼각형은 전체 24개(6×4)로 분할할 수 있겠네요? 24는 4의 배수이기도 하고요. 저, 방법을 찾았어요!"
-
![[개념쏙쏙! 수학] 다양한 도형, 어떻게 하면 똑같이 나눌 수 있을까](http://newsteacher.chosun.com/site/data/img_dir/2015/07/29/2015072903818_4.jpg)
- ▲ /그림=이창우
"네. 그리고 하나의 도형도 여러 가지 도형이 더해진 것처럼 느껴져요."
"맞아. 그래서 건축가나 다양한 분야의 디자이너들은 공간 감각을 기르기 위해 도형 분할 연습을 많이 한단다. 용도나 아름다움에 맞추어 공간을 다양하게 활용할 수 있으니까."
[관련 교과] 4학년 2학기 '사각형과 다각형', 6학년 1학기 '여러 가지 입체 도형'
[함께 생각해봐요]
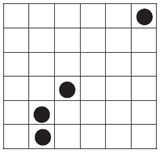
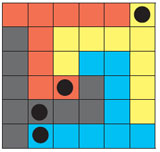
아래와 같은 도형을 주어진 선을 따라서 모양과 크기가 같은 4개의 도형으로 분할해 보세요. 또 각각의 도형이 검은 점 하나씩 가질 수 있도록 분할해 보세요.
답: