신문은 선생님

"아빠, 곱셈을 이용해 전신 마비 환자와도 대화하는 방법을 개발했대요."

"어디 보자, 사람이 두 자릿수끼리 곱셈하는 것 같은 집중력이 필요한 연산을 할 때 동공이 커진다는 것을 이용했구나. 환자가 '예'라고 대답하고 싶으면 24×32 같은 두 자릿수 곱셈을 암산하도록 하고, '아니요'라고 대답하고 싶으면 가만히 있도록 해서 의사 표현을 할 수 있도록 했다니 신기하네."

"네. 곱셈을 하며 집중할 때 동공이 커진다는 것은 처음 알았어요. 하지만 '예'와 '아니요'로만 의사 표현을 할 수 있으니, 표현할 수 있는 게 별로 없어서 정말 답답하겠어요."

"'예' '아니요'만 표현할 수 있어도 우리 예상보다 아주 많은 대화를 할 수 있어."

"겨우 두 가지 의사 표현일 뿐인데요?"

"하하. 그림, 게임, 음악, 계산 등 못하는 분야가 없는 컴퓨터도 알고 보면 0과 1, 두 가지만 가지고 모든 것을 표현하는데?"

"0과 1만 가지고 어떻게 그런 복잡한 게임을 만들어요?"

"잘 생각해보면 수학도 처음엔 1에서 시작했다고 할 수 있어. 하나와 하나가 더해지면 둘이 된다는 개념이 발전해서 덧셈, 뺄셈, 곱셈, 나눗셈의 사칙연산을 만들었지. 우리 동현이는 '비트'라는 말 들어봤니?"

"네. 컴퓨터를 16비트, 32비트, 64비트 등으로 구분하잖아요?"

"비트는 정보를 표현하는 최소 단위인데 쉽게 말해 '불을 켜고 끌 수 있는 램프의 수'를 의미한다고 할 수 있어. 자, 예를 들어 램프에 불이 하나 들어오는 것을 '1'이라고 한다면 4를 나타내는 데는 램프가 몇 개 필요할까?"

"램프에 불이 4개 들어와야 하니 당연히 4개가 필요하겠지요."

"그래. 초기의 인류는 수를 나타낼 때 이런 방식을 사용했어. 1을 선 하나로 나타냈다면 4는 선 4개로 나타낸 것이지. 하지만 99 같은 수를 나타내기 위해서는 선을 99번 그어야 했기 때문에 표현하는 것이 힘들었고, 읽는 것도 어려울 수밖에 없었어. 그래서 만들어진 것이 바로 '진법'이야. 우리는 지금 0에서 9까지의 숫자만으로 모든 수를 표현할 수 있지? 그것은 9 다음에 자릿수를 바꿔 10으로 놓는 방식, 즉 10진법을 사용하기 때문이지. 그런데 컴퓨터도 10진법을 이용하면 램프 27개로 0에서 999까지 표현할 수 있지. 예를 들어 538 같은 경우는 이렇게 표현해."

○○○○●●●●● 5

○○○○○○●●● 3

○●●●●●●●● 8

"아, 각 자리에 9개씩 램프를 배치하면 되는군요. 그래도 램프 27개로 999까지 나타낸다면 컴퓨터에는 엄청나게 많은 램프가 필요하겠어요."

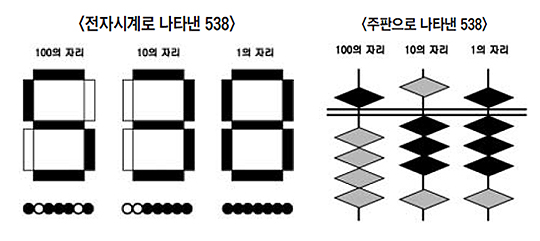
"그래서 초기의 컴퓨터는 집채만큼 컸지. 이런 단점을 보완하기 위해 컴퓨터 개발자들은 더 적은 램프로 더 많은 수를 나타내는 방식을 연구했어. 전자시계의 표현 방식도 그중 하나야. 전자시계를 잘 보면 시, 분, 초를 나타내는 각 자리에 막대 7개가 있고 그 막대로 숫자 모양을 만들어 0에서 9까지 나타내잖아?"

"아하! 맞아요. 그러고 보니 이런 방식으로 999까지 나타내면 램프 수를 7+7+7=21, 21개로 줄일 수 있네요?"

"그런데 주판은 이보다 더 효율적이야. 주판은 알이 위아래로 움직이는 방식으로 수를 나타내는데 아래쪽에는 네 알, 위쪽에는 한 알로 되어 있지. 그래서 아래 네 알이 다 올라간 다음 위의 알을 올리고 아래 알을 전부 내리고 다시 하나씩 올려 9까지 나타내. 신기하지? 이런 방식은 999까지 나타내는 데 램프를 5+5+5=15, 15개로 줄일 수 있어."

"와. 그럼 지금의 컴퓨터는 이것보다 램프 수를 더 줄였나요?"

"물론이야. 컴퓨터는 램프 하나로 두 가지 부호를 나타낼 수 있음을 활용해, 각 자리를 2진수로 나타내면 램프 10개만으로 1024까지 표현할 수 있어. 예를 들어 1 다음 수는 2인데 2를 나타낼 수 없으므로 다음 자리의 수를 올리고 1의 자리를 0으로 놓는 방식이야. 즉, 1 다음에는 10이고, 그다음 수는 11, 그다음 수는 100이 되는 거지. 이런 방식으로 수를 나타내면 램프가 늘어날 때마다 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 식으로 나타낼 수 있는 수의 범위가 2배씩으로 늘어나. 지금의 개인용 컴퓨터에는 램프 32개(32비트)나 64개(64비트)를 쓰는 방식을 주로 이용하고 있는데, 32개는 0에서 4294967295까지 나타낼 수 있고, 64개는 0에서 18446744073709551615까지 나타낼 수 있어."

"놀라워요."

"그래. 하지만 컴퓨터가 나타내는 수를 사람이 읽기 어렵다는 단점이 있어. 10진법으로 쓴 1000을 컴퓨터는 1111101000으로 나타내기 때문에 컴퓨터 전문가라도 수를 읽거나 쓰기 어렵지. 그래서 프로그램을 만든 후에는 그 숫자를 컴퓨터가 이해할 수 있는 방식인 '기계어'로 번역하는 과정이 필요하단다."

"정말 신기하네요. 우리가 사용하는 컴퓨터에 이런 원리가 숨어 있었다니."

[함께 생각해봐요]

램프를 이용해 문자를 표현하려 합니다. 램프는 켜고 끄는 두 가지 신호를 나타낼 수 있다고 한다면 영문 알파벳과 숫자를 모두 나타내는 데는 램프가 최소 몇 개 필요할까요?

답: 6개. 한 램프가 두 가지 신호를 나타내므로 두 램프로는 2×2=4, 네 가지 신호를 나타낼 수 있어요. 알파벳은 26개 문자, 숫자는 10개 문자이므로 36가지 신호가 필요합니다. 즉 최소한 램프 6개(2×2×2×2×2×2=64)가 필요합니다. 실제 컴퓨터의 경우는 알파벳과 숫자를 따로 인식할 수 있는 전환 버튼(시프트)을 이용해 램프 5개(2×2×2×2×2=32)로 알파벳과 숫자를 모두 나타낼 수 있어요.


[관련 교과] 6학년 2학기 '경우의 수와 확률'