개념쏙쏙! 수학

겨울방학을 맞아 아인이네 가족은 신라시대의 역사가 숨 쉬는 경주로 여행을 떠났어요. 그곳에서 첨성대, 불국사, 석굴암, 안압지 등을 보면서 선조의 건축 기술을 떠올리게 됐죠.

"아인이는 이번 경주 여행에서 어느 곳이 가장 기억에 남았니?"

"하나만 꼽는다면 석굴암요. 아치형 모양의 석굴암 내부가 아름답고 놀라웠어요."

"석굴암의 놀라운 건축 기술의 기본에는 수학이 숨어 있단다. 만약 수학적 계산 없이 건물을 지었다면, 지금의 석굴암뿐만 아니라 많은 유산을 볼 수 없었을 거야."

"수학은 생각보다 오래전부터 우리 생활 곳곳에 쓰이고 있었네요. 그럼 이전에도 제가 배우는 수학책으로 공부한 건가요?"

"하하, 아니. 선조가 배웠던 책은 지금과는 조금 달랐어. 이 중에서 현재 전해지는 가장 유명한 책으로 '구장산술(九章算術)'이 있어. 구장산술은 중국에서 전해져 온 수학책인데, 아홉 장으로 구분된 다양한 주제에 수학 246문제와 해설이 들어 있지."

"그런데 왜 옛날에도 수학을 배워야 했나요?"

"예전에는 농경 사회였기 때문에 많은 사람이 농사를 지었단다. 그래서 관리들이 세금을 물리려면 땅의 넓이, 농작물 수확량 등을 계산해야 했지."

"그럼, 어떤 내용이 있었나요?"

"아홉 장으로 나뉘어 있다고 했지? 각 장 내용은 다음과 같아. 넓이, 비율, 입체의 부피, 방정식, 피타고라스 정리, 삼각함수 등 아인이가 아직 배우지 않은 내용도 상당히 많이 있구나."

"또한 그때는 우리가 현재 쓰는 수학 기호 대신 문장을 썼어. 자, 그럼 제1장에서 원 모양 토지의 넓이를 한번 구해볼까? 아인이가 관리가 돼 토지 측량을 해야 하는 상황이라고 생각하고 구장산술에 있는 문제를 풀어봐. '둥그런 땅이 있습니다. 땅 둘레는 30보, 지름은 10보라고 할 때, 땅의 넓이는 얼마일까요?' 문제에서 '보'는 성인 남성의 보폭으로 한 걸음을 뜻한단다."

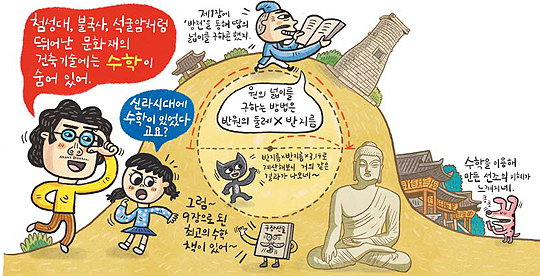
"원의 넓이를 구하는 거네요. 원의 넓이는 '반지름×반지름×원주율'이니까 '5보×5보×3.14=78.5보²'이 나와요."

"잘했구나. 그럼 아빠가 당시 계산법으로 계산해볼게. 그 당시에는 원의 넓이를 '반원의 둘레×반지름'으로 계산했다고 해. 그래서 '15보×5보=75보²'이 나오는 거지. 또한 원 둘레를 원의 지름으로 나눈 원주율이 약 3이 된다는 것을 알고 있었다고 해. 그래서 지금과 같은 공식에 대입해 봐도 비슷한 결과가 나오지."

"계산 결과가 큰 차이가 없다니 정말 대단해요. 다른 문제도 풀어보고 싶어요."

"하하. 그럼 이번에는 제2장에 있는 곡물의 물물교환 문제를 계산해볼까? '좁쌀과 벼는 50대 60으로 교환할 수 있습니다. 그렇다면 벼 12두 6(14/15)승을 가진 사람은 좁쌀 얼마와 교환할 수 있을까요?' 여기서 1두(斗)는 10승(升)의 단위와 같단다."

"이건 비례식으로 풀면 되겠네요. 좁쌀:벼=50:60=□:12두6(14/15) 승이니까 6×□=5×12두6(14/15) 승이 되어서, □=12두 6(14/15)승×(5/6)=10두5(7/9)승이 나와요."

"응. 맞았어. 옛날 풀이에서는 비례식을 만들어 풀진 않았지만, 벼의 양에 5를 곱하고 6으로 나눠 12두6(14/15)승×(5/6)로 좁쌀의 양을 계산했단다. 결국 계산 원리는 같았던 거지."

"그 당시 관리들에게 정말 필요한 문제가 많이 수록돼 있네요. 이런 수학책이 삼국시대부터 있었고, 관리들이 체계적인 수학 공부를 통해 세금을 매겼다는 사실이 놀라운데요."

"세금을 물려야 하거나, 성을 쌓거나 토지를 측량해야 하는 관리들에게는 필독서와 같은 것이었다고 해. 모든 사람에게 공평하게 정책을 시행해야 할 때 수학만큼 정확한 것도 없지. 구장산술은 동양 수학의 기본이자 동양 수학 발달에 선구적인 역할을 했어. 그래서 서양 수학의 기본서인 '유클리드의 원론'과 비교되기도 한단다."

[함께 생각해봐요]

아래는 구장산술의 제3장 ‘쇠분’에 해당하는 문제입니다. 옛날에 ‘대부’ ‘불경’ ‘잠뇨’ ‘상조’ ‘공사’의 다섯 계급에 속하는 사람들은 각각 ‘5:4:3:2:1’의 비율로 소득을 나누어 가졌다고 합니다. 이들이 다 같이 사냥을 가서 5마리의 노루를 얻었다고 가정할 때, 노루의 마릿수를 계급에 따라 나누어 보세요.

해설: 비례배분에 따라 각각 대부: 5×(5/15)=5/3마리, 불경 : 5×(4/15)=4/3마리, 잠뇨 : 5×(3/15)=1마리, 상조 : 5×(2/15)=2/3마리, 공사 : 5×(1/15)=1/3마리의 사슴을 나누어 가질 수 있습니다.

[관련 교과] 6학년 1학기 '원주율과 원의 넓이' '연비와 비례 배분'