개념쏙쏙! 수학

"엄마 아빠랑 함께 영화를 보니 더 재미있었어요. 특히 주인공들이 미로를 탈출하기 위해 사투를 벌이는 장면은 정말 박진감 넘치더라고요."

부모님과 미로가 나오는 영화를 본 예원이가 신난 표정으로 말했어요.

"그런데 만약에 제가 미로에 갇힌다면 정말 암담할 것 같아요."

"그래? 엄마는 미로에서 탈출하는 방법을 알고 있는데, 예원이도 가르쳐 줄까?"

그러자 아빠께서 깜짝 놀란 표정으로 말씀하셨어요.

"당신도 미로 탈출법을 알아? 나도 한 가지 아는데. 그럼 우리 서로 알고 있는 방법을 공유해 볼까?"

아빠의 제안에 엄마께서 자신만만한 미소를 지으셨어요.

"좋아. 내가 아는 방법은 미로에서 지나갈 필요가 없는 길을 지워 나가면서 숨겨진 길을 찾는 방법이야. 예를 들어 그림 1과 같은 미로가 있다고 가정해 봐. 만약 어떤 공간의 3면이 벽으로 둘러싸였다면 그곳은 막다른 골목이므로 지워야 해. 왜냐하면 미로를 통과하는 도중에 그곳을 지나간다면 들어오는 방향과 나가는 방향으로 최소 2개의 공간과 연결되어야 하거든. 그런데 그림 2처럼 3면이 막힌 곳을 지우고 나면 그와 이웃한 공간 가운데 새로 만들어지는 막다른 골목도 있단다. 그런 공간까지 차례차례 지우다 보면 그림 3과 같이 간단한 길만 남아서 쉽게 미로를 빠져나올 수 있어."

"우아, 정말 신기해요. 이 방법을 쓰면 어떤 미로든 금세 탈출할 수 있겠네요!"

"그렇지? 하지만 이 방법에는 한 가지 단점이 있어. 지금처럼 미로의 전체 지도를 보고 풀 때는 유용하지만, 실제로 미로에 갇혀서 전체 지도를 볼 수 없는 상황에서는 쓸모없다는 거야."

"아, 생각해 보니 정말 그렇네요. 그럼 이번엔 아빠가 아는 방법을 얘기해 주세요. 그 방법은 실제로 미로에 갇혔을 때도 쓸 수 있을까요?"

"그럼! 아빠가 아는 방법은 아주 간단한 데다 실제로 미로를 탈출하는 데도 유용하단다. 미로의 입구부터 출구까지 오른쪽 또는 왼쪽의 한쪽 벽면만 계속 따라가면 되거든."

"네? 그런 방법으로 미로를 빠져나올 수 있다고요? 믿을 수가 없는데요?"

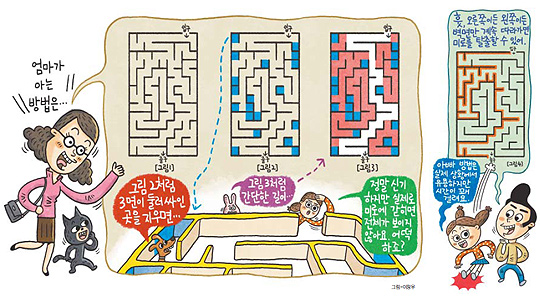
"정말이란다. 아까 엄마가 설명한 그림 1의 미로를 입구부터 오른쪽 벽면만 계속해서 따라가 보렴. 그러면 그림 4와 같이 미로를 탈출할 수 있어. 오른쪽이 아닌 왼쪽 벽만 계속 따라가도 마찬가지로 탈출할 수 있지. 이렇게 하면 실제 미로에서도 빠져나올 수 있지만 이 방법에도 단점이 하나 있단다."

"아! 그건 제가 알 것 같아요. 엄마의 방법보다 훨씬 먼 길을 가야 하니까, 미로가 크고 복잡해지면 시간이 굉장히 오래 걸린다는 점이지요?"

"맞아! 예원이는 관찰력이 아주 뛰어나구나."

"두 방법 모두 단점이 있긴 하지만 이런 방법을 찾아낸 사람들은 정말 대단하네요."

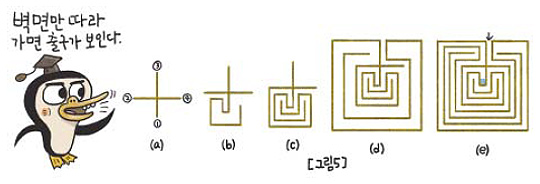
"엄마와 아빠가 말한 두 가지 방법은 모두 '위상(位相)'이라는 수학 개념을 통해 찾은 것이란다. '위상'은 예원이가 대학생이 되어 수학을 전공하기 전에는 배우지 않지만, 간단한 예시만으로도 미로 문제를 푸는 데 필요한 개념을 이해할 수 있어. 그림 5의 (a)와 같이 십자가 모양을 그리고 각각의 선 ①~④를 서로 교차하지 않게끔 차례로 연장하여 (e)와 같은 미로를 그려보자. (e)는 (a)에서 선의 길이만 늘였을 뿐 달리 변한 것이 없지. 따라서 (e)의 입구로 들어간 후 계속 앞으로 나아가면 가장 안쪽 공간으로 들어갈 수 있어. 마찬가지로 그림 1의 미로도 실제로 가야 하는 길을 쭉 편다고 생각하면 오른쪽(또는 왼쪽) 벽만 따라가서 출구로 나가는 것이 가능하다는 점을 알 수 있단다."

"와, 오늘은 제가 마치 책에서나 보던 대단한 수학자가 된 것 같은 기분이에요. 저도 집에 가서 책에 나온 미로를 풀어보며 저만의 미로 탈출법을 찾아봐야겠어요. 하하."

[함께 생각해봐요]

‘위상수학’에서는 어떤 물체를 구멍 내거나 새로 연결하지 않고, 구부리거나 늘이거나 줄이는 식의 변형만으로 만들 수 있는 물체를 모두 같은 형태라고 봅니다. 예를 들어 고무찰흙과 접시, 손잡이가 있는 컵과 도넛을 같은 형태로 보지요. 위상수학의 시각으로 볼 때, 우리 주위에서 손잡이가 있는 컵과 같은 형태인 물건을 3개만 찾아보세요.

정답: 반지, 타이어, 옷걸이 등.


[관련 교과] 6학년 2학기 '경우의 수와 확률'